| 余割 | 您所在的位置：网站首页 › 三角函数sec csc cot特殊值 › 余割 |
余割
|
余割（Cosecant， csc {\displaystyle \csc} ）是三角函数的一种。它的定义域不是整个实数集，值域是绝对值大于等于1的实数。它是周期函数，其最小正周期为 2 π {\displaystyle 2\pi} 。在单位圆上，余割函数位于割线上，因此将此函数命名为余割函数。 目录 1 定义 1.1 直角三角形定义 1.2 平面直角坐标定义 1.3 单位圆定义 1.4 级数定义 1.5 微分定义 1.6 指数定义 2 恒等式 2.1 与其他三角函数的关系 2.2 和差恒等式 2.3 倍半角公式 3 微积分 4 拓展阅读 定义[] 直角三角形定义[]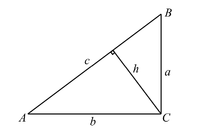 直角三角形定义 在直角三角形中，一个锐角 ∠ A {\displaystyle \angle A} 的余割定义为它的斜边与对边的比值，也就是： csc A = c a {\displaystyle \csc A = \frac {c}{a}\,\!}其定义和正弦函数互为倒数。 平面直角坐标定义[]设 θ {\displaystyle \theta} 是平面直角坐标系xOy中的一个象限角， P ( x , y ) {\displaystyle P\left( {x,y} \right )} 是角的终边上一点，则 θ {\displaystyle \theta} 的余割定义为： csc θ = r y {\displaystyle \csc \theta = \frac{r}{y}} 单位圆定义[] 单位圆的两种定义 在平面坐标系中，有一个以原点为圆心半径为一个单位长度的圆（即单位圆）。设一个过原点的线，同x轴正半部分得到一个角 θ {\displaystyle \theta} （逆时针方向的度量是正角而顺时针的度量是负角），并与单位圆相交于A点。余割可以通过以下两种方式定义： 记单位圆与y轴的交点为E，过E作垂直于y轴的直线，该直线于OA延长线交于一点P，则OP的长度为该角余割的绝对值（一、二象限为正值；三、四象限为负值）。（图中蓝线） 过A点做一直线，与单位圆相切，直线与y轴的交点与原点之间的距离即为该角度的余割值（一、二象限为正值；三、四象限为负值）。（图中绿线） 级数定义[] csc x = ∑ n = 0 ∞ ( − 1 ) n + 1 2 ( 2 2 n − 1 − 1 ) B 2 n x 2 n − 1 ( 2 n ) ! = 1 x + x 6 + 7 x 3 360 + 31 x 5 15120 + ⋯ ( 0 x = − csc x cot x {\displaystyle \csc ' x=-\csc x \cot x} csc x = ( ln | csc x − cot x | ) ′ {\displaystyle \csc x =\left( \ln \left |\csc x - \cot x\right | \right) '} 指数定义[] csc θ = 2 i e i θ − e − i θ {\displaystyle \csc \theta = \frac{2\mathrm{i}}{e^{{\mathrm{i}}\theta} - e^{-{\mathrm{i}}\theta}} \,} 恒等式[] 与其他三角函数的关系[]说明：以第一象限角为例，注意其余象限角的符号处理。 函數 sin {\displaystyle \sin} cos {\displaystyle \cos} tan {\displaystyle \tan} cot {\displaystyle \cot} sec {\displaystyle \sec} csc {\displaystyle \csc}csc θ {\displaystyle \csc \theta } 1 sin θ {\displaystyle {1 \over \sin \theta} } 1 1 − cos 2 θ {\displaystyle {1 \over \sqrt{1 - \cos^2 \theta}} } 1 + tan 2 θ tan θ {\displaystyle {\sqrt{1 + \tan^2\theta} \over \tan \theta} } 1 + cot 2 θ {\displaystyle \sqrt{1 + \cot^2 \theta} } sec θ sec 2 θ − 1 {\displaystyle {\sec \theta \over \sqrt{\sec^2\theta - 1}} } csc θ {\displaystyle \csc \theta\ } 和差恒等式[] csc ( α ± β ) = csc α csc β cot β ± cot α {\displaystyle \csc(\alpha\pm\beta)=\frac{\csc\alpha\csc\beta}{\cot\beta\pm\cot\alpha}} 倍半角公式[] csc 2 θ = csc 2 θ 2 cot θ = sec θ csc θ 2 {\displaystyle \begin{align} \csc 2\theta &= \frac{\csc^2\theta}{2\cot\theta} \\ &= \frac{\sec\theta\csc\theta}{2} \end{align}} csc 3 θ = csc 3 θ 3 csc 2 θ − 4 {\displaystyle \csc 3\theta =\frac{\csc^3\theta}{3\csc^2\theta-4}} csc θ 2 = ± 2 sec θ sec θ − 1 {\displaystyle \csc \frac{\theta}{2} = \pm\, \sqrt{\frac{2\sec\theta}{\sec\theta - 1}}} 微积分[] 拓展阅读[] 三角恒等式 |
）是三角函数的一种。它的定义域不是整个实数集，值域是绝对值大于等于1的实数。它是周期函数，其最小正周期为
2
π
{\displaystyle 2\pi}
。在单位圆上，余割函数位于割线上，因此将此函数命名为余割函数。
的余割定义为它的斜边与对边的比值，也就是：
是平面直角坐标系xOy中的一个象限角，
P
(
x
,
y
)
{\displaystyle P\left( {x,y} \right )}
是角的终边上一点，则
θ
{\displaystyle \theta}
单位圆定义[]
csc
x
=
(
ln
|
csc
x
−
cot
x
|
)
′
{\displaystyle \csc x =\left( \ln \left |\csc x - \cot x\right | \right) '}
指数定义[]
csc
θ
=
2
i
e
i
θ
−
e
−
i
θ
{\displaystyle \csc \theta = \frac{2\mathrm{i}}{e^{{\mathrm{i}}\theta} - e^{-{\mathrm{i}}\theta}} \,}
恒等式[]
与其他三角函数的关系[]
cos
{\displaystyle \cos}
tan
{\displaystyle \tan}
cot
{\displaystyle \cot}
sec
{\displaystyle \sec}
csc
{\displaystyle \csc}
倍半角公式[]
csc
2
θ
=
csc
2
θ
2
cot
θ
=
sec
θ
csc
θ
2
{\displaystyle \begin{align}
\csc 2\theta &= \frac{\csc^2\theta}{2\cot\theta} \\ &= \frac{\sec\theta\csc\theta}{2}
\end{align}}
csc
3
θ
=
csc
3
θ
3
csc
2
θ
−
4
{\displaystyle \csc 3\theta =\frac{\csc^3\theta}{3\csc^2\theta-4}}
csc
θ
2
=
±
2
sec
θ
sec
θ
−
1
{\displaystyle \csc \frac{\theta}{2} = \pm\, \sqrt{\frac{2\sec\theta}{\sec\theta - 1}}}
微积分[]
拓展阅读[]
三角恒等式
【本文地址】